For any normally distributed random variable (X), the z-score corresponding to any particular value of the random variable is given by the formula,
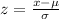
The mean of the normal distribution is 425,
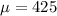
The standard deviation of the normal distribution is 51,

Then the formula of z-score becomes,
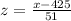
a)
Given the value of the random variable as 268,
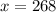
The corresponding z-score will be,
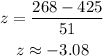
Thus, the required z-score is -3.08 approximately.
b)
Given the value of the random variable as 512,
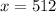
The corresponding z-score will be,
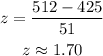
Thus, the required z-score is 1.70 approximately.
c)
Given the value of the random variable is 450,
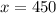
The corresponding z-score will be,
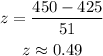
Thus, the required z-score is 0.49 approximately.