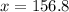Question

A rocket is launched from the ground and travels in a straight path. The angle of inclination of the rocket's path is 1.1 radians. (That is, the rocket's path and the ground form an angle with a measure of 1.1 radians.)What is the slope of the rocket's path?   If the rocket has traveled 66 yards horizontally since it was launched, how high is the rocket above the ground? ____yards   At some point in time the rocket is 308 yards above the ground. How far has the rocket traveled horizontally (since it was launched) at this point in time? _____yards

Answer 1

the given problem can be exemplified in the following diagram:

The slope is defined as the tangent of the angle, therefore the slope is:

`\begin{gathered} m=\tan 1.1 \\ m=1.96 \end{gathered}`

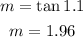
Therefore, the slope is 1.96.

When the rocket has travelled 66 yards, we have the following situation:

To determine the value of the height "y" we can use the function tangent since this function is defined as:

`\tan x=(opposite)/(adjacent)`

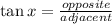
Replacing the known values:

`\tan 1.1=(y)/(66)`

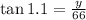
Multiplying both sides by 66 we get:

`66\tan 1.1=y`

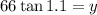
Solving the operations:

`129.7=y`

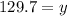
Therefore, the height is 129.7 yards.

When the rocket is at a height of 308 yards, we have the following situation:

we can use the tangent function. Replacing the known values we get:

`\tan 1.1=(308)/(x)`

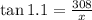
Multiplying both sides by "x":

`x\tan 1.1=308`

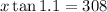
Dividing both sides by tan 1.1:

`x=(308)/(\tan 1.1)`

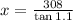
Solving we get:

`x=156.8`