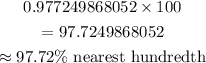Question

People spend an average of 7 hours per day on their home computers with a standard deviation of 1hour. What proportion spends at least 5 hours per day on their home computers? (enter the answeras a percent rounded to the nearest hundredth as needed)

Answer 1

Solution;

From the given question, we have

`\begin{gathered} \mu=7 \\ \sigma=1 \end{gathered}`

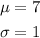
To evaluate the proportion of people that spend at least 5 hours per day on their home computers,

Step 1: Evaluate the z score value.

The z score value is expressed as

`\begin{gathered} z=(x-\mu)/(\sigma) \\ where \\ x\implies sample\text{ value} \\ \mu\implies mean\text{ value} \\ \sigma\implies standard\text{ deviation} \end{gathered}`

In this case,

`x=5`

thus, we have the z score value to be evaluated as

`z=(5-7)/(1)=-2`

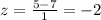
Step 2: Evaluate the probability that people will spend at least 5 hours per day on their home computers,

From the normal distribution table, we have

This implies that

`P(x\ge5)=P(z\ge-2)=0.977249868052`

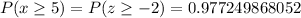
Hence, the proportion that spends at least 5 hours per day on their home computers is evaluated to be

`\begin{gathered} 0.977249868052*100 \\ =97.7249868052 \\ \approx97.72\%\text{ \lparen nearest hundredth\rparen} \end{gathered}`