Question

Use what you know about special right triangles to find the area of each regular polygon. Leave youranswer in simplest form.

Answer 1

The first step to find the area of the hexagon is to find the apothem of it by using the following formula:

`a=(l)/(2tan\theta)`

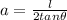
Where l is the sidelength and θ is half the central angle:

`a=((16√(3))/(3))/(2tan30)=8`

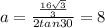
Now, find the perimeter of the hexagon by multiplying the side length by 6:

`\begin{gathered} P=6\cdot(16√(3))/(3) \\ P=32√(3) \end{gathered}`

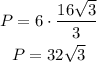
Finally, find the area of the hexagon by using the following formula:

`\begin{gathered} A=(P\cdot a)/(2) \\ A=(32√(3)\cdot8)/(2) \\ A=128√(3) \end{gathered}`

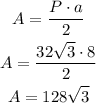
The area of the given hexagon is 128√3