The amount in the account after six years is $15,448
Here, we want to calculate the amount that would result from compounding a deposit
To calculate this, we shall be using the compound interest formula
That would be;
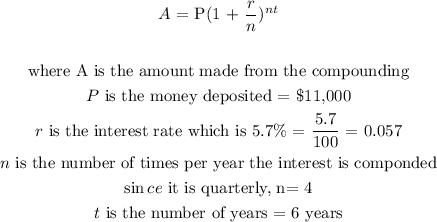
Substituting all these values into the equation, we have that;
