The equation of a parabola with vertex (h,k) is:

Where a is a constant.
Rewrite the given expression in vertex form by completing the square:
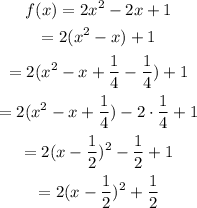
Use the expression in vertex form to answer parts a to c.
a)
To find the y-intercept, evaluate f at x=0:

The axis of symmetry is a vertical line that passes through the vertex. Since the coordinates of the vertex are (1/2,1/2), then the equation of the axis of symmetry is:
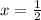
And the x-coordinate of the vertex is 1/2.
b)
Use the values x=0, x=0.5, x=1, x=1.5, x=2 to make a table:
![undefined]()