Question

In the relationship shown by the data linear? If so , model the date with an equation A. The relationship is linear; y-1=4/5(x-5) B. The relationship is linear; y-5= 5/4( x-1 ) C. The relationship is not linear D. The relationship is linear; y-5 = -4/5( x-1 )

Answer 1

The general equation of a line is given as

`\begin{gathered} y=mx+c \\ \text{where} \\ m=Gradient \\ c=\text{intercept} \end{gathered}`

To calculate the slope/gradient of two points (x1,y1) and (x2,y2) is gotten as

`m=(y_2-y_1)/(x_2-x_1)`

From the table in the question, we will pick any two points

`\begin{gathered} (x_1,y_1)=(1,5) \\ (x_2,y_2)=(5,10) \end{gathered}`

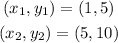
By substituting the values, we will have

`\begin{gathered} m=(10-5)/(5-1) \\ m=(5)/(4) \end{gathered}`

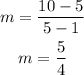
To calculate the equation of a line when the gradient/slope (m) is given and a point also is given, we will use the formula

`m=(y-y_1)/(x-x_1)`

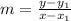
Let's take the points (x1,y1) to be ( 1,5) we will have the equation of the line to be

`\begin{gathered} (5)/(4)=(y-5)/(x-1) \\ by\text{ cross multiplying, we will have} \\ y-5=(5)/(4)(x-1) \end{gathered}`

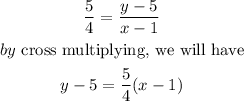
Therefore,

The relationship is linear ; y-5=5/4(x-1)

The correct answer is OPTION B