SOLUTION
The formula for finding the amount of carbon 14 remaining in time t is given by

To get a, we use the information that the half-life is 5730 years. That is in 5730 years,

Therefore;
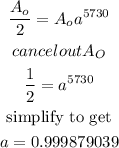
And;
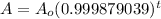
b. To find when the object died given that it has 63% of its Carbon 14 remaining today.

Therefore, the correct answer is option e. 3819.5 years