Question

Graph the line with the points (-1,6), slope 5/4

Answer 1

Given:

A line passes throught the point (-1,6).

The slope of the line is m = (5/4).

The objectiv is to find the equation of the line.

Step-by-step explanation:

Consider the coordinates as,

`(x_1,y_1)=(-1,6)_{}`

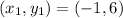
The general formula to fid the equation of line in slope-point form is,

`y-y_1=m(x-x_1)\text{ . }\ldots\ldots\ldots(1)`

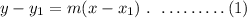
Now, substitue the given values in equation (1).

`\begin{gathered} y-6=(5)/(4)(x-(-1)) \\ y-6=1.25(x+1) \\ y=1.25x+1.25+6 \\ y=1.25x+7.25\text{ . . . .(2)} \end{gathered}`

To obtain the graph:

Consider two value for the x = 0 and y = 0 to obtain coordinates to draw the graph.

At x = 0:

Substitute the value of x in equation (2),

`\begin{gathered} y=1.25(0)+7.25 \\ y=7.25 \end{gathered}`

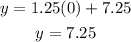
Thus, the coordinate is (0,7.25).

At y = 0:

Substitute the value of y in equation (2),

`\begin{gathered} 0=1.25x+7.25 \\ x=(-7.25)/(1.25) \\ x=-5.8 \end{gathered}`

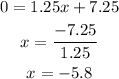
Thus, the coordinate is (-5.8,0).

To plot the graph:

The graph of the line will be,

Hence, the graph of the line y = 1.25x + 7.25 is obtained.