The given expression is
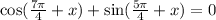
Let's apply the sum identity to each one
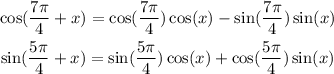
Then, we replace these expressions
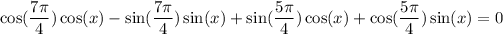
Now, we evaluate the expressions where x = 90°. Also, we know that pi = 180°.
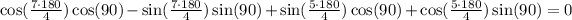
If we solve and simplify, we get
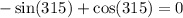
But, sin(315) = cos(315), so their difference is zero.
Hence,
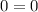
The identity is proven.
Hence, the identity required was the sum identity for sine and cosine.