Question

For the following set of data, find the number of data within i population standarddeviation of the mean.Data Frequency10114121512191820131029331

Answer 1

Find the mean of the given data. Multiply the number of frequencies to its corresponding data value. For the denominator, find the total number of frequencies.

`\begin{gathered} \bar{x}=(10(1)+12(6)+14(12)+\cdots29(6)+33(1))/(1+6+12+\cdots+6+1) \\ =(1499)/(79) \\ \approx18.97 \end{gathered}`

Find the standard deviation. Substitute the values into the following formula.

`\begin{gathered} \sigma=\sqrt[]{\frac{f_1(x_1-\bar{x})^2+f_2(x_2-\bar{x})^2+\cdots+f_n(x_n-\bar{x})^2}{N}} \\ =\sqrt[]{(1(10-18.97)^2+6(12-18.97)^2+12(14-18.97)^2+\cdots+6(29-18.97)^2+1(33-18.97)^2)/(79)} \end{gathered}`

Simplify the expression.

`\begin{gathered} \sigma\approx\sqrt[]{(80.4609+48.4809+24.7009+\cdots+100.6009+196.8409)/(79)} \\ \approx\sqrt[]{(517.4281)/(79)} \\ \approx6.55 \end{gathered}`

To obtain the number of data within 1 population standard deviation, add and subtract the obtained standard deviation from the mean.

`\begin{gathered} \bar{x}+\sigma=18.97+6.55=25.52 \\ \bar{x}-\sigma=18.97-6.55=12.42 \end{gathered}`

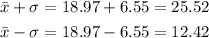
Thus, the range of 1 standard deviation away from the mean is (25.52,12.42).

Therefore, add the frequencies from 13 to 25.

`12+12+18+13=55`

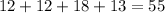
Therefore, there is 55 data 1 standard deviation away from the mean.