ANSWER:
4 meters
Explanation:
We have that the work-energy theorem says that the work done by the force acting on a body modifies its kinetic energy, therefore:
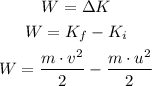
The car comes to rest after a given distance, so v = 0.
Work is is the constant force acting on an object over a distance traveled determined by the angle between the force and the displacement, but since the friction force acts in the opposite direction to the direction of motion in this case, the work is equal to the product of force and distance.
Therefore:
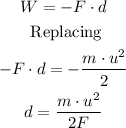
We have:
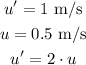
Therefore:
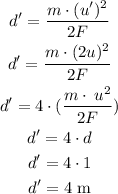
Therefore, the car travels a distance of 4 meters