Answer:
(x-4)x = 0
Explanation:
If we have a quadratic equation of the form

it has solutions at x = a and x = b because putting either one of these values into the above equation satisfies it. For example, putting in x = a gives
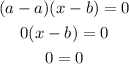
this satisfies the equation and likewise for x = b.
Hence, if we want to construct an equation which has solutions x = 4 and x = 0, we just need to set a = 4 and b = 0. Doing this gives

which is a polynomial that has the solutions desired.