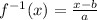Given the function:
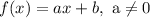
For each value of x, then there is only one value for f(x). Thus, the function is one-to-one.
Then, let's find the inverse function.
To find the inverse, substitute f(x) by x in x by 0:
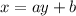
Now, solve for y by subtracting b from both sides:
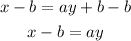
And divide both sides by a:

Finally, substitute y by f⁻¹(x):
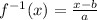
Answer: The function is one-to-one and the inverse is: