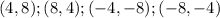Question

The square of the sum of two numbers is 144 and the sum of their squares is 80. Find the numbers.(Use completing the square method)

Please help me

Answer 1

(4,8);(8,4);(-4,-8);(-8,-4)

Explanation:

Ok, let's start writing down the two conditions:

`\left \{ {(x+y)^2 = 144} \atop {x^2+y^2=80}} \right.`

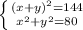
Mumble. The second almost look like a square, if only there was the
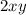`2xy` term. Let's add (and subtract, so we aren't creating something new) term to the second:

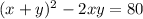`(x+y)^2-2xy = 80` But we know what the first term is, it's 144. Let's replace and do some number tricks to get:
`144-2xy=80 \rightarrow 72-xy=40\\72-40=xy \rightarrow xy=32`

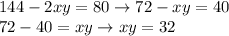
At this point, let' stare at it for a while. You can tell that the system is simmetrical (if you replace x with y you still get a solution). Moreover, x and y have the same sign: it means that if (a,b) is a solution, then also (b,a), (-a,-b) and (-b, -a) are solutions, and since it's a 4th degree system (the degree of a system is the product of the degrees of the single equations, and they're both quadratic) there are no other solution.

Let's find one pair then. We're tasked to find two numbers that sum to
`√(144) = 12` and whose product is 32. that is, the root of the polynomial

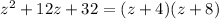`z^2+12z+32= (z+4)(z+8)` (or if you can't see the factors right away, bruteforce it with quadratic formula, it's always good practice). That tells us that one of the two is -4, and the other is -8. From what we said above, the solutions are by combining them with plus or minus.

`(4,8);(8,4);(-4,-8);(-8,-4)`

Answer 2

Explanation:

(x + y)^2 = 144

x^2 + y^2 = 80

----

x + y = 12 ---> y = 12 - x

x^2 + y^2 = 80

x^2 + (12-x)^2 = 80

2x^2 - 24x + 64 = 0

x^2 - 12x + 32 = 0

x = 4, x = 8

y = 8, y = 4

============================

x + y = -12 ---> y = -12 - x

x^2 + y^2 = 80

x^2 + (-12-x)^2 = 80

2x^2 + 24x + 64 = 0

x^2 + 12x + 32 = 0

x = -4, x = -8

y = -8, y = -4

-------------

One number is + or -4, the other is + or -8,

and the absolute value of the sum is 12.