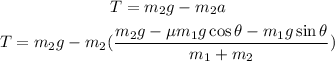Question

Block 1 of mass mi is at rest on a plane that makes an angle of 0 with the horizontal. Thecoefficient of kinetic friction between the block and the plane is p. The block is attachedto block 2 of mass me that hangs freely by an inextensible, light string that passes over africtionless, massless pulley. When the blocks are released, block 1 moves up the inclinewhile block 2 moves down. See Figure 1 for the diagram of the two blocks.m,m2Figure 1: Two blocks connected by a string, with one block resting on an inclined plane.By drawing the free body diagram for each mass and applying Newton's laws, calculate:i) the magnitude of the acceleration of the blocks.ii) the tension in the string connecting the two blocks.

Answer 1

The force diagram of the given system is shown below:

where,

N: normal force = Wy

Wy: component of the weight W perpendicular to the incline = Wcosθ

Wx: component of the weight W parallel to the incline = Wsinθ

W: weight of block 1 = m1*g

W2: weight of block 2 = m2*g

T: tension on the cord

Fr: friction force = μN

i) The acceleration of the two blocks is the same.

The sum of forces on the first block along the direction of the incline is (equation 1):

`\begin{gathered} T-F_r-W_x=m_1\cdot a \\ T-\mu N-m_1g\sin \theta=m_1\cdot a \end{gathered}`

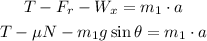
The sum of forces along the direction perpendicular to the incline is (equation 2):

`\begin{gathered} W_y+N=0 \\ N=W_y=m_1g\cos \theta \end{gathered}`

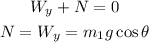
The sum of forces on the second block is (equation 3):

`m_2g-T=m_2\cdot a`

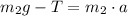
Now, add the first and third equation, solve for a, and replace the expression for N, as follow:

`\begin{gathered} T-\mu N-m_1g\sin \theta+m_2g-T=m_1a+m_2a \\ a(m_1+m_2)=m_2g-\mu N-m_1g\sin \theta \\ a=(m_2g-\mu m_1g\cos\theta-m_1g\sin\theta)/(m_1+m_2) \end{gathered}`

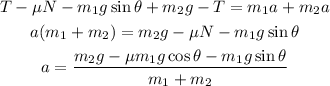
The previous expression is the result for the acceleration of the two blocks.

ii) And the tension is:

`\begin{gathered} T=m_2g-m_2a \\ T=m_2g-m_2((m_2g-\mu m_1g\cos\theta-m_1g\sin\theta)/(m_1+m_2)) \end{gathered}`