From the given problem, the position of the plane is at :
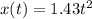
First step is to determine the velocity.
Velocity is the 1st derivative of the position.
Note that the general differentiation is :

The velocity will be :
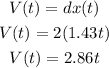
Acceleration is the 1st derivative of the velocity.
So it follows that :

Therefore, the answer is 2.86 m/s^2