Question

An AM radio listener is located 5.0 km from the radio station.Part AIf he is listening to the radio at the frequency of 660 kHz, how many wavelengths fit in the distance from the station to his house?

Answer 1

11 wavelengths

Step-by-step explanation

Given:

• The distance between the radio station and the listener, 5 km = 5000 m

,

• The broadcasting frequency, f = 660 kHz = 660000 Hz

Unknown:

• The number of wavelengths that fit in the distance from the station to the listener's house

First, we have to find the wavelength,

`\lambda=(c)/(f)`

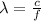
Where c is the speed of light in m/s and f is the frequency in Hz,

`\lambda=(3\cdot10^8m/s)/(660000Hz)\approx454.55m`

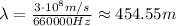
To find how many wavelengths fit in the distance from the station to the listener's house, we have to divide the distance between them by the wavelength of the wave,

`n=(5000m)/(454.55m)\approx11`

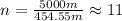
Hence, a total of 11 wavelengths fit in the distance from the station to his house.