Question

An aluminum cup (a = 24 x 106 °C¹) sitting outside on a summer day (T= 33°C) can hold a maximum of 285 mL of a liquid. How much liquid can the glass hold on a cold day (T= -4°C)? How much liquid can it hold on a spring day (T = 17°C)?

Answer 1

`\begin{gathered} (a)\text{ }285.76\text{ }mL \\ \\ (b)\text{ }284.67\text{ }mL \end{gathered}`

Step-by-step explanation

Parameters given:

Linear expansivity of aluminum, α = 24 * 10^(-6) C^(-1)

Initial temperature,m T1 = 33°C

Initial volume of liquid, V1 = 285 mL

(a) To find the amount of liquid that the cup can hold on a summer day, apply the formula for volume expansivity:

`3\alpha=(V_2-V_1)/(V_1(T_2-T_1))`

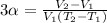
where T2 = temperature on a cold day

V2 = volume on a cold day

Therefore, solving for V2, we have that the volume that the cup can hold on a cold day will be:

That is the answer.

(b) To find the volume that the cup can hold on a spring day, apply the same formula but for T2 = 17°C:

`\begin{gathered} 0.000072=(V_2-285)/(285(17-33)) \\ \\ 0.000072=(V_2-285)/(285*-16)=(V_2-285)/(-4560) \\ \\ V_2-285=0.000072*-4560=-0.32832 \\ \\ V_2=285-0.32832 \\ \\ V_2=284.67\text{ }mL \end{gathered}`

That is the answer.