Question

The graph of a function f(x) passes through the following points:(0, - 2),(1,0), (- 1, –4)Which of the following could be f(x)?

Answer 1

Hello!

First, let's make a graph with these points:

As we can see, it is a function in the form ax + b = 0 (1st degree).

To solve this exercise, we can calculate the slope and then write the equation of the line in the slope-intercept form.

So, let's calculate the slope:

`Slope=(y_B-y_A)/(x_A-x_B)=(0-(-2))/(1-0)=(+2)/(1)=2`

Now, let's write it in the slope-intercept form as y = mx + b:

• m, is the slope

,

• b ,is the y-intercept

,

• x ,and ,y ,are generic coordinates

To solve it, let's replace x and y with the coordinates of point C (third):

`\begin{gathered} y=mx+b \\ y=2\cdot x+b \\ -4=2\cdot(-1)+b \\ -4=-2+b \\ -4+2=b \\ b=-2 \end{gathered}`

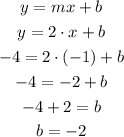
Now, we know all unknows, let's rewrite it:

`\begin{gathered} y=mx+b \\ y=2x-2 \end{gathered}`

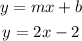
Oops! But we don't have this option, right?

So, we must remember one thing: when we are talking about functions, f(x) and y mean the same.

So, we just have to replace y with f(x) and the answer will be:

`f(x)=2x-2`