Question

Which of the following polar pairs could also be a representation of (3, 120°)? 3 answers

Answer 1

The given coordinate pair is (3, 120°)

We know that the coordinate pair (r,x) is equivalent to (r, 360°n + x) and (-r, 180°(2k + 1) + x), where n and r are integers.

So, first we assume that the radius is positive and find the equivalent angles of 120°:

`\begin{gathered} 120=1(360)+120=480 \\ and \\ 120=-1(360)+120=-360+120=-240 \end{gathered}`

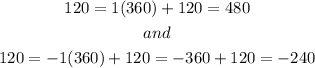
So, the polar coordinate (3, 120°) is equivalent to (3, 480°) and (3, -240°).

- Now, we find the equivalent coordinates with the negative radius:

`\begin{gathered} (-3,180(2*(-1)+1)+120)=(-3,180(-2+1)+120 \\ =(-3,180(-1)+120)=(-3,-180+120)=(-3,-60) \end{gathered}`

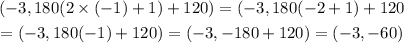
Consequently, (-3, -60°) is also a representation of the given polar pair.

Answer: A, B and D