From the graph, let's write the equations for f(x) and g(x).
Apply the slope-intercept form of linear equations:
y = mx + b
Where m is the slope and b is the y-intercept.
• For f(x):
To find the slope apply the slope formula:

Take two points on the line of f(x):
(x1, y1) ==> (0, -1)
(x2, y2) ==> (-2, 0)
Thus, we have:

The y-intercept (b), is the point the line crosses the y-axis.
Therefore, the y-intercept for f(x) is at b = -1
Therefore, the equation for f(x) is:

• For g(x):
Take two points on the line of g(x).
(x1, y1) ==> (-2, 0)
(x2, y2) ==> (2, 2)
Apply the slope formula to find the slope:
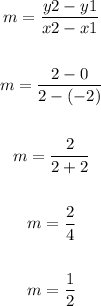
The y-intercept of g(x) is: b = 1
Therefore, the equation for g(x) is:
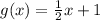
To determine the reflection that transforms f(x) to g(x):
From the graph, we can see the red line represents f(x) while the blue line is that of g(x).
Apply the transformation rules for functions.
When f(x) becomes -f(x), there is a reflection over the x-axis.
Here, the parent function f(x) becomes -f(x) = g(x)
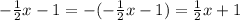
Therefore, there was a reflection over the x-axis that transforms the grah f(x) to g(x).
ANSWER:
• f(x) = -½x - 1
,
• g(x) = ½x + 1
• Reflection over the x-axis.