Answer
The length is 35 inches
The width is 9 inches
Solution
- This question leads to a simultaneous equation with the length and width as variables.
- For the first equation, we simply need to interpret the logic in the question.
- For the second equation, we should apply the formula for the perimeter of a rectangle since we have been given the perimeter of the rectangle to be 88 inches.
- Thus, we can solve the question as follows:
First Equation

Second Equation
- Now, let us apply the formula for the perimeter of a rectangle to find the second equation
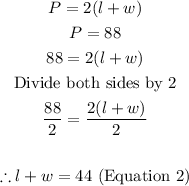
- Now, let us solve the equations simultaneously.
- We can use the substitution method as follows:

Final Answer
The length is 35 inches
The width is 9 inches