Question

Write a system of equations to describe the situation below, solve using any method, and fill in the blanks. The drama club is selling gift baskets to raise money for new costumes. During the fall play, they sold a combined 26 regular gift baskets and 12 deluxe gift baskets, earning a total of $1,166. During the spring musical, they sold 19 regular gift baskets and 8 deluxe gift baskets, earning a total of $819. How much are they charging for the different sized gift baskets?

Answer 1

Let be "r" the amount of money (in dollars) they are charging for a regular gift basket and "d" the amount of money (in dollars) they are charging for a deluxe gift basket.

Based on the information given in the exercise, you can set up the following System of equations:

`\begin{cases}26r+12d=1,166 \\ 19r+8d=819\end{cases}`

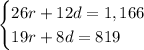
You can solve the System of equations using the Substitution method:

1. Solve for "r" from the second equation:

`\begin{gathered} 19r+8d=819 \\ 19r=819-8d \\ r=(819-8d)/(19) \end{gathered}`

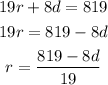
2. Substitute the new equation into the first original equation.

3. Solve for "d" in order to find its value.

Then:

`\begin{gathered} 26r+12d=1,166 \\ \\ 26((819-8d)/(19))+12d=1,166 \\ \\ 26((819-8d)/(19))=1,166-12d \\ \\ (21,294-208d)/(19)=1,166-12d \\ \\ 21,294-208d=(19)(1,166-12d) \\ 21,294-208d=22,154-228d \\ -208d+228d=22,154-21,294 \\ 20d=860 \\ \\ d=(860)/(20) \\ \\ d=43 \end{gathered}`

4. Knowing the value of "d", you can substitute it into the following equation, and then you must evaluate in order to find the value of "r":

`r=(819-8d)/(19)`

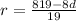
Then, this is:

`\begin{gathered} r=(819-8(43))/(19) \\ \\ r=(819-344)/(19) \\ \\ r=(475)/(19) \\ \\ r=25 \end{gathered}`

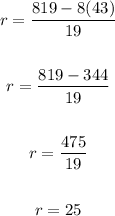
The answer is: They are charging $25 for a regular gift basket and $43 for a deluxe gift basket.