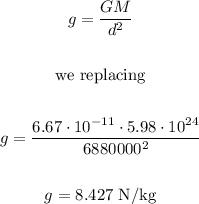ANSWER:
a) 7614.11 m/s
b) 8.427 N/kg
Explanation:
Given:
Height (h) = 5.0 x 10^5 m
Radius of the earth (r) = 6.38 x 10^6m
Mass of earth (M) = 5.98 x 10^24kg
Mass of satellite (m)
a)
We can calculate the speed of the satellite by taking into account the following:
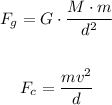
In this case, the gravitational force and the centripetal force are equal, therefore:

b)
Now, we calculate the gravitational field at that height, like this: