Solution:
Given:
To get the equation, we pick two points to get the rate of change of depth per day.
Using the points (1,18) and (2,17.5), then
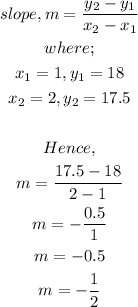
Using the form of a linear equation,
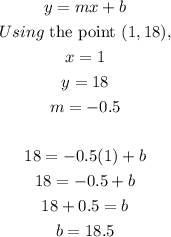
Hence,
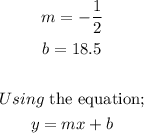
Therefore, the equation that shows the water depth, y in the fish tank after x days is;
