Question

Gravel pouring from a chute at a rate of 26 cubic feet per minute forms a conical pilewhose height is always twice the radius. How fast is the height of the pile increasing atthe instant when the pile is 50 feet high?

Answer 1

Given:

The rate of change of volume of the cone V = 26 cubic feet per minute.

We need to find the rate of change of height at height = 50 feet.

The height = twice the radius.

`h=2r`

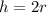
Divide both sides by 2, we get

`(h)/(2)=(2r)/(2)`
`r=(h)/(2)`

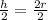
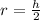
Consider the volume of the cone.

`V=(1)/(3)h\pi r^2`
`\text{Substitute }r=(h)/(2)\text{ in the formula.}`

`V=(1)/(3)h\pi((h)/(2)_{})^2`

`V=(1)/(3)h\pi(h^2)/(4)`

`V=(\pi)/(12)h^3`

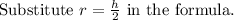
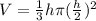
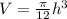
Differentiate with respect to t.

`(dV)/(dt)=(\pi)/(12)*3h^2*(dh)/(dt)`
`\text{Substitute }(dV)/(dt)=26\text{ and }h=50\text{ in the equation.}`

`26=(\pi)/(12)*3(50)^2*(dh)/(dt)`

`26=1962.5*(dh)/(dt)`

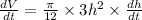
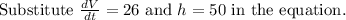
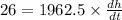
Dividing both sides by 1962.5, we get

`(26)/(1962.5)=(dh)/(dt)`

`(dh)/(dt)=0.0132\text{ f}eet\text{ per minute}`

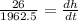
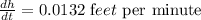
The height of the pile is increasing by 0.01 feet per minute at the instant when the pile is 50 feet high.