Given data
The length of the major axis(l) of the ellipse is
![l=4\sqrt[]{194\text{ }}\text{units}](https://img.qammunity.org/2023/formulas/mathematics/college/89hkm1qa12f62hs506r3241izql683dkhk.png)
The length of the minor axis of the ellipse is
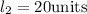
The formula for the length of the major axis is,
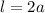
The formula for the length of the minor axis is
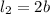
Solving for a
![4\sqrt[]{194}=2a](https://img.qammunity.org/2023/formulas/mathematics/college/biz91k32rb7d5g5hytmgmkapyav3ffn5co.png)
We are told to look for how far apart are the vertices of the hyperbola.
The formula to solve for the distances between the vertices of the hyperbola is given as,
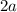
which is equal to the length of the major axis.
Hence, the distances between the vertices of the hyperbola is
![4\sqrt[]{194}units](https://img.qammunity.org/2023/formulas/mathematics/college/pl5f40qlt62mwh9fwk6qlxswnqg9gn35nj.png)