Question

use properties of logarithms to expand the logarithmic expression as much as possible.a. 12-log4 xb. 3-log4 xc. 3/xd. -3 log4 x

Answer 1

`\text{Log}_4((64)/(x))=3-Log_4x`

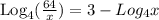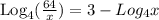
Here, we want to use logarithmic properties to expand the given expression;

We are going to use the following properties of logarithms;

`\text{Log}_a((x)/(y))=Log_ax-Log_ay`

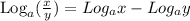
Applying that in the case of the question, we have;

`\text{Log}_4((64)/(x))=Log_464-Log_4x`

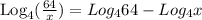
Furthermore;

`Log_aa^2=2Log_aa_{_{}}_{}`

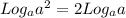
Kindly recall that;

`64=4^3`

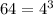
Thus, we have;

`\text{Log}_464=Log_44^3=3Log_44`

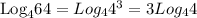
Also, an important logarithmic property to use is that;

`Log_aa=1_{}`

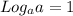
Thus, we have;

`3og_44\text{ = 3}`

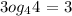
So finally we have;

`\text{Log}_4((64)/(x))=3-Log_4x`