Answer::
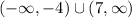
Explanation:
Given the function:
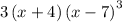
We want to determine the interval in which the function is greater than 0.
First, solve for the critical values.
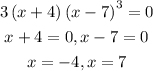
So, the following are the possible intervals:
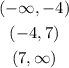
We test each of the intervals:
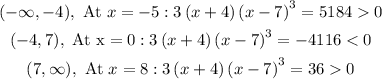
Therefore, the function is greater than zero in the intervals:
The result can be confirmed using the graph below: