Question

Assume that x has a normal distribution with the specified mean and standard deviation. Find the indicated probability. (Round your answer to four decimal places.) = 109; = 11P(x ≥ 120) = ___

Answer 1

To answer this question, we can use the standard normal distribution to find the probability for x > 120. We can proceed as follows:

1. We need to find the z-score for the given raw value of 120.

2. We know that the z-score is given by:

`z=(x-\mu)/(\sigma)`

Where

• x is the raw value (x = 120).

,

• μ is the population's mean. In this case, μ = 109.

,

• σ is the population standard deviation. In this case, σ = 11.

Therefore, we have that the z-score is:

`z=(120-109)/(11)\Rightarrow z=1`

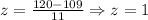
We can see that the value for z = 1. It means that the value is one standard deviation above the mean of the population.

If we use a cumulative standard normal distribution table, and we find the value for z = 1, we will have a cumulative probability of:

`P(z<1)=0.8413`

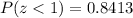
However, we are looking for P(z > 1). Therefore, to find this value, we can proceed as follows:

`P(z>1)=1-P(z<1)=1-0.8413`

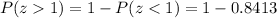
Therefore:

`P(z>1)=0.1587`

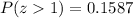
We need to remember that this value of z is a "transformation" of the value 120 into the standard normal distribution.

In summary, we can say that:

`P(x>120)=0.1587`