Question

A cylindrical oil tank holds about 785 cubic feet of oil and has a height of 10 feet. The formula for the volume of a cylinder is V = (pie symbol)r2h. Find the radius of the tank. Use 3.14 for (pie symbol).

Answer 1

We have that the formula for the volume of a cylinder is:

`v\text{ = }\pi\cdot r^2\cdot h`

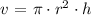
Where Volume = V = 785 ft³

Heigth = h = 10 ft

Radius = r = ?

Pi = π = 3.14

Replacing these values:

`785\text{ = 3.14 }\cdot r^2\cdot10`

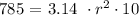
Solve the equation for r :

Divide by 10 and 3.14 into both sides

785/(10)(3.14) =3.14*(r ^2)*10/ (3.14)(10)

785 / (10)(3.14) = (r ^2)

`(785)/(10\cdot3.14)=r^2`

`(785)/(31.4)=r^2`
`25=r^2`

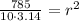
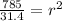
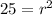
Use square root on both sides:

`\sqrt[2]{25}=\sqrt[2]{r^2}`

Then:

`5ft\text{ = r}`

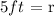
This means that the radius of the tank is equal to 5 feet.