The first step to solve the problem is to graph the equation:
To create the graph we need to create a table with a few ordered pairs. We will use the values of x going from 0 to 10 in increments of 1.
We have:
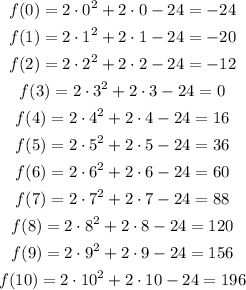
We calculated the points now we need to graph the function.
The zeros of the function are the points at which it crosses the "x" axis. This functtion crosses the axis at he points "-4" and "3".