The shape comprises a semicircle, rectangle, and a trapezoid
A) The shape below will illustrate how the side length of the rectangle will be calculated
Part I is the semicircle of diameter
![\begin{gathered} d=8\operatorname{cm} \\ r=(d)/(2) \\ r=(8)/(2)=4\operatorname{cm} \end{gathered}]()
From the diagram above
![AB=r=4\operatorname{cm}]()
To find the missing side length of the rectangle , we will use the relation below
![AB+BC+CD=12\operatorname{cm}]()
Where.
![\begin{gathered} AB=4\operatorname{cm} \\ CD=3.5\operatorname{cm} \end{gathered}]()
By substituting the values, we will have
![\begin{gathered} AB+BC+CD=12\operatorname{cm} \\ 4+BC+3.5=12\operatorname{cm} \\ 7.5+BC=12\operatorname{cm} \\ BC=12-7.5 \\ BC=4.5cm \end{gathered}]()
The missing side length of the rectangle is = 4.5 cm
Hence,
The rectangle can be represented below as
The formula for the area of the rectangle is
![\begin{gathered} A_{\text{rectangle}}=\text{length}* breadth \\ \text{where,} \\ \text{length}=8\operatorname{cm} \\ \text{breadth}=4.5\operatorname{cm} \end{gathered}]()
By substituting the values, we will have
![\begin{gathered} A_{\text{rectangle}}=\text{length}* breadth \\ A_{\text{rectangle}}=8\operatorname{cm}*4.5\operatorname{cm} \\ A_{\text{rectangle}}=36\operatorname{cm}^2 \end{gathered}]()
Hence,
The Area of the rectangle = 36cm²
B) To calculate the area of the semicircle, we will use the formula below
![\begin{gathered} A_{\text{semicircle}}=(\pi* r^2)/(2) \\ \text{where,} \\ r=4\operatorname{cm} \end{gathered}]()
By substituting the values , we will have
![\begin{gathered} A_{\text{semicircle}}=(\pi* r^2)/(2) \\ A_{\text{semicircle}}=(\pi*4^2)/(2)=(16\pi)/(2)=8\pi \\ A_{\text{semicircle}}=25.13\operatorname{cm}^2 \end{gathered}]()
Hence,
The area of the semicircle = 25.13 cm²
To calculate the area of the trapezoid, we will use the formula below
![\begin{gathered} A_{\text{trapezoid}}=(1)/(2)(a+b)* h \\ \text{where,} \\ a=8\operatorname{cm} \\ b=15\operatorname{cm} \\ h=3.5\operatorname{cm} \end{gathered}]()
The diagram below represents the trapezoid
By substituting the values, we will have
![\begin{gathered} A_{\text{trapezoid}}=(1)/(2)(a+b)* h \\ A_{\text{trapezoid}}=(1)/(2)(8\operatorname{cm}+15\operatorname{cm})*3.5\operatorname{cm} \\ A_{\text{trapezoid}}=(1)/(2)(23\operatorname{cm})*3.5\operatorname{cm} \\ A_{\text{trapezoid}}=\frac{80.5\operatorname{cm}}{2} \\ A_{\text{trapezoid}}=40.25\operatorname{cm}^2 \end{gathered}]()
Hence,
The area of the trapezoid is = 40.25cm²
To calculate the total area of the shape, we will use the formula below
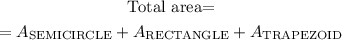
By substituting the values, we will have
![\begin{gathered} \text{Total area=}A_{\text{SEMICIRCLE}}+A_{\text{RECTANGLE}}+A_{\text{TRAPEZOID}} \\ \text{Total area}=25.13\operatorname{cm}+36\operatorname{cm}+40.25\operatorname{cm}^2 \\ \text{Total area}=101.38\operatorname{cm}^2 \end{gathered}]()
Hence,
The Total Area of the composite shape = 101.38cm²