We have to use the formula for the area of a triangle
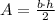
Where A = 10,710 and h = 612, let's find b
Now, we use the base and height, which are legs, to find the hypotenuse using Pythagorean's Theorem
![\begin{gathered} h^2=612^2+35^2 \\ h=\sqrt[]{374,544+1,225} \\ h=\sqrt[]{375,769} \\ h=613 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/9e52whz9ycopzfytrar9z9so6btcsxwxip.png)
Hence, the hypotenuse of the right triangle is 613 inches.