Question

In 1900 the population of a certain town was 1500 people. Assume an annual growth rate of 6%. Find the population in 1950.

Answer 1

You have the following formula given in the exercise:

`P\mleft(t\mright)=1500\mleft(1+r\mright)^t`

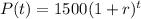
Where "r" is the annual growth rate (expressed as a decimal) and "t" is the time in years.

Based on the information given in the exercise, you know that the annual growth rate is 6%.

`r=(6)/(100)=0.06`

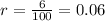
Notice that 6% can be expressed as a decimal number by dividing it by 100.

Since the information provided is from 1900 to 1950, you can identify that:

`t=50`

Now you can substitute values into the formula and evaluate:

`P(50)=1500(1+0.06)^(50)\approx27,631`

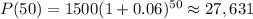
Therefore, the answer is: Option a.