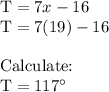Question

Please help me with this qurstion

Answer 1

The value of
`x` is
`19`.

Angle R's measure is
`43^(\circ)`.

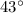Angle S' measure is
`20^(\circ)`.

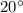Angle T's measure is
`117^(\circ)`.

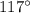Explanation:

Step 1: Construct expressions for the angles in terms of x

The angle R is said to be five more than twice x, which means that 5 is added to 2x:

`\text{R}=5+2x`

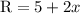
The angle S is said to be one more than x, which means that 1 is added to x:

`\text{S}=1+x`

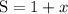
The angle T is said to be sixteen less than seven times x, which means that 16 is subtracted from 7x:

`\text{T}=7x-16`

Step 2: Create an equation with all the expressions

Since there are three angles in the shape, it is clearly a triangle.

The sum of angles of a triangle is
`180^(\circ)`.

Which means that the sum of the expressions above, would equal to
`180`:

`(5+2x)+(1+x)+(7x-16)=180`

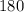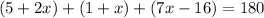
Step 3: Solve the equation

The equation is:

`(5+2x)+(1+x)+(7x-16)=180`

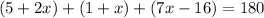
Upon solving it, we get:

`(5+2x)+(1+x)+(7x-16)=180\\\\\text{Remove the brackets:}\\5+2x+1+x+7x-16=180\\\\\text{Add the like terms:}\\10x-10=180\\\\\text{Add 10 on both sides of the equation:}\\10x-10+10=180+10\\\\\text{Simplify:}\\10x=190\\\\\text{Divide by 10 on both sides of the equation:}\\(10x)/(10)=(190)/(10)\\\\\text{Simplify:}\\x=19`

Step 4: Calculate the measure of the angles

With
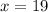`x=19`, substitute and calculate the angle R:

`\text{R}=5+2x\\\text{R}=5+2(19)\\\\\text{Calculate:}\\R=43^(\circ)`

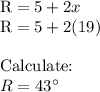
Calculate the angle S:

`\text{S}=1+x\\\text{S}=1+19\\\\\text{Calculate:}\\\text{S}=20^(\circ)`

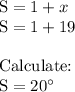
Calculate the angle T:

`\text{T}=7x-16\\\text{T}=7(19)-16\\\\\text{Calculate:}\\\text{T}=117^(\circ)`