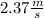Question

A spring has a resting length of 0.50 m and a spring constant of 955N/m. A 1.70 kg block collides with a spring and compresses the spring to 0.10m. Find the initial speed of the block

Answer 1

A spring with a constant k stores potential energy when it is compressed a distance x. That potential energy is given by the formula:

`U=(1)/(2)kx^2`

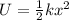
On the other hand, that potential energy comes from the kinetic energy of the block. If the block has a mass m and an initial speed v, then its kinetic energy is equal to:

`K=(1)/(2)mv^2`

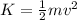
Substitute k=955 N/m and x=0.10 m to find the potential energy stored in the spring after the collision:

`\begin{gathered} U=(1)/(2)(955(N)/(m))(0.10m)^2 \\ =(1)/(2)(955(N)/(m))(0.01m^2) \\ =(1)/(2)\cdot9.55N\cdot m \\ =4.775J \end{gathered}`

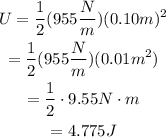
Isolate v from the equation for the kinetic energy of the block:

`v=\sqrt[]{(2K)/(m)}`

Since all the potential energy of the spring corresponds to the initial kinetic energy of the block, substitute K=4.775J and m=1.70kg to find the initial speed of the block:

Therefore, the initial speed of the block is:

`2.37(m)/(s)`