Question

If 1.113 is the 2-unit growth factor what is the 1-unit percent change? %If 0.609 is the 3-unit growth factor what is the 1-unit percent change?If 0.655 is the 4-unit growth factor what is the 5-unit percent change?If 35% is the 1/3 unit percent change what is the 1-unit percent change? %

Answer 1

EXPLANATION

Given that 1.113 is the 2-unit growth factor:

The percent growth over previous n unit time periods is called n-unit growth.Thus, if the n-unit growth in percent (xn%) is given, we can find average 1-unit growth in percent (x1%) as follows:

`Unit-\text{Growth factor:}\cdot(1+(x_n)/(100))=(1+(x_1)/(100))^n`

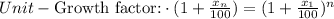
In this case, we need to replace

`Unit-\text{Growth factor:}\cdot(1+(x_n)/(100))=(1+(1.113)/(100))^2`
`Unit-\text{Growth factor:}\cdot(1+(x_n)/(100))=1.02238`

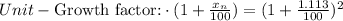
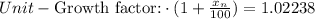
Subtracting by 1:

`(x_n)/(100)=1.02238-1`

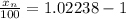
Multiplying both sides by 100:

`x_n=(1.02238-1)\cdot100`
`x_n=0.0223838\cdot100`

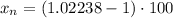
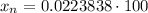
Multiplying terms:

`x_n=2.23`

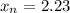
The answer is 2.23%.