Step 1: State the given in the question
Given that 3 out 20 cars passing through an intersection did not fully stop
Step 2: State what to be determined
We are to determine the probability that a car arriving at this intersection that will not fully stop
Step 3: State the formula for finding probability
The formula for finding the probability of an en event, E, from a sample S, is the ratio of the number of elements of event E to the total number of elements in the sample S.
This can be represented mathematically as

Step 4: Use the formula to solve the probability
If the event E is cars passing through an intersection did not fully stop. Then, the number of elements in the event E is given as 3. That is:
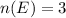
The sample is the total number of cars, which is given as 20. This means that
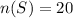
Therefore, the probability of the event occuring would be P(E). This is as calculated below:
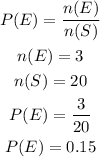
Hence, the probability that a car arriving at this intersection will not fully stop is 3/20 or 0.15