Question

Jason jumped off of a cliff into the ocean in Acapulco while vacationing with some friends. His height above ocean measured in feet as a function of time could be modeled by the function h(t) = -16t2 + 16t + 672, where t is the time in seconds and h is the height in feet. After how many seconds did Jason hit the water

Answer 1

You have the following function for the height respect to the water, Jason has after time t he jumped:

`h(t)=-16t^2-16t+672`

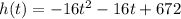
In order to determine the time Jason takes to hit the water, equal h = 0. Thus, you have a quadratic equation and it is necessary to find the zeros of the polynomial:

`0=-16t^2-16t+672`

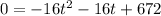
use the following quadratic formula to find the zeros:

`t=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

where a,b and c are the coefficients of the polynomial:

a = -16

b = -16

c = 672

replace these values into the formula:

`\begin{gathered} t=\frac{-(-16)\pm\sqrt[]{(-16)^2-4(-16)(672)}}{2(-16)} \\ t=\frac{16\pm\sqrt[]{43264}}{-32} \\ t=(16\pm208)/(-32) \\ t=-0.5\pm(-6.5) \end{gathered}`

Then, you obtain the following two values:

`\begin{gathered} t=-7 \\ t=6 \end{gathered}`

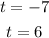
Select the positive values because negative time does not have physical meaning.

Hence, Jason takes 6 seconds to hit the water.