Given::
Length = 6.00 m
Weight of beam = 155 N
Angle = 30.0 degrees
Weight added at the right-end = 100 N
If the system is in equilibrium, let's find the weight, w, at the left-end.
Since the system is in equilibrium, the net torque of the system will be zero.
Now, we have the equation:
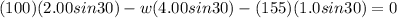
Where w is the weight at the left end.
Let's solve for w.
We have:
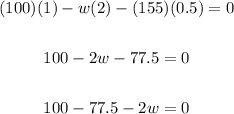
Solving further:
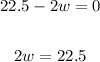
Divide both sides by 2:
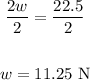
Therefore, the weight hung at the left end is 11.25 N
ANSWER:
11.25 N