1 Answer

Alessandro Gaballo · Answer 1 · 2023-12-11T04:30:00+0000

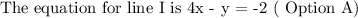
$\text{The equation for line I is 4x - y = -2 ( Option A)}$

The equation for the second line is:

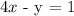
$4x\text{ - y = 1}$
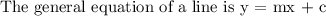
$\text{The general equation of a line is y = mx + c}$

Where m = slope and c = Intercept

Let us rewrite the given equation in that form :

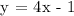
$\text{ y = 4x - 1}$

Comparing y = 4x - 1 with y = mx + c:

m = 4 and c = -1

Since line I is parallel to the given line, it means their slopes are equal. Therefore, the slope for line I is also m = 4

Line I contains the Point:

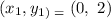
$(x_1,y_{1)\text{ = }}(0,\text{ 2)}$

The equation of a line can also be written in the form:

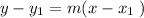
$y-y_1=m(x-x_{1\text{ }})$
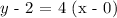
$y\text{ - 2 = 4 (x - 0)}$
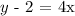
$y\text{ - 2 = 4x}$

By rearranging the above equation:

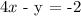
$4x\text{ - y = -2}$

The above is the equation for line I

Please log in or register to add a comment.