Question

The principal would like to assemble a committee of 5 students from the 15-memberstudent council. How many different committees can be chosen?

Answer 1

The question involves combination since it only deals with the selection without arrangement.

Hence the formula to use is

`^nC_r=(n!)/((n-r)!r)`

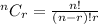
For this question, we have

`\begin{gathered} n=15,r=5 \\ ^nC_r=(n!)/((n-r)!r) \\ \text{becomes } \\ ^(15)C_5=(15!)/((15-5)!5!) \end{gathered}`

Simplifying the last expression we obtained

`\begin{gathered} ^(15)C_5=(15!)/(10!5!) \\ =(15*14*13*12*11*10!)/(10!*5!) \\ =3003 \end{gathered}`

Therefore,

The number of committees to be chosen is 3003