Question

Which function has the greatest average rate of change over the given interval?

Answer 1

Answer: C(x) > a(x) , meaning c(X) has the greatest average rate of change over the given interval.

Explanations :

• The greatest average rate of change = slope

,

• given by formula :

`m\text{ = }(y_2-y_1)/(x_2-x_1)`

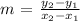
(a) For a(x),

`\begin{gathered} minitial\text{ = }\frac{-2+3\text{ }}{0+1\text{ }} \\ \text{ = 1/1} \\ \text{ = 1 } \end{gathered}`
`\begin{gathered} m\text{ final = }(13-6)/(3-2) \\ \text{ = }7\text{ } \end{gathered}`

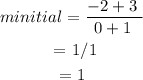
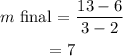
• The average rate of change over the given interval = 7-1 = 6

(b) for b(x) , we have

`\begin{gathered} M\text{ initial = }(3-1)/(0+1) \\ \text{ = 2} \end{gathered}`

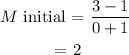
and

`\begin{gathered} m\text{ final = }\frac{9-7\text{ }}{3-2\text{ }} \\ \text{ = 2} \end{gathered}`

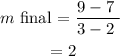
• We can see that b(x) has constant average rate of change at 2 , therefore this will not be considered for this purpose of the exercise.

(c) for C(x) , we have

`\begin{gathered} M\text{ initial = }(-1+2)/(0+1) \\ \text{ = 1 } \end{gathered}`

and

`\begin{gathered} m\text{ final = }\frac{13-5\text{ }}{3-2} \\ \text{ = }8\text{ } \end{gathered}`

• The average rate of change over the given interval =, 8 -1 = 7

in conclusion , C(x) = 7 , whereas a(x) = 6 ,

Therfore C(x) > a(x)