Question

Hey, I’m really having trouble with this question and could use some help.

Answer 1

From the given graph, we have 2 points with coordinates:

`\begin{gathered} (x_1,y_1)=(1,2) \\ \text{and} \\ (x_2,y_2)=(4,1) \end{gathered}`

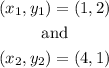
The equation of a line in slope-intercept form is given by

`y=mx+b`

With the given points, we can find the slope m as follows:

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ \text{then} \\ m=(1-2)/(4-1) \end{gathered}`

which gives

`m=(-1)/(3)=-(1)/(3)`

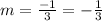
Then, our line equation has the form

`y=-(1)/(3)x+b`

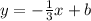
Now, we can find the y-intercept b by substituting one of the two given points. For instance, if we substitute point (1,2) into the last result, we get

`2=-(1)/(3)(1)+b`

which gives

`\begin{gathered} 2=-(1)/(3)+b \\ \text{then} \\ 2+(1)/(3)=b \\ (7)/(3)=b \end{gathered}`

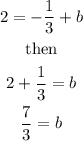
then, the line equations is

`y=-(1)/(3)x+(7)/(3)`

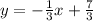
a) The linear function is

`f(x)=-(1)/(3)x+(7)/(3)`

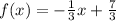
b) What is f(6)?

In this case, we have that x=6. Then, by replacing this value into our function, we get

`f(6)=-(1)/(3)(6)+(7)/(3)`

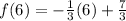
which gives

`\begin{gathered} f(6)=-(6)/(3)+(7)/(3) \\ f(6)=(-6+7)/(3) \\ f(6)=(1)/(3) \end{gathered}`

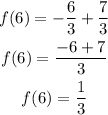
therefore, the answer for part b is

`(1)/(3)`