Question

Determine if the line passing through A(7,5) and B(-14, -9) is parallel, or perpendicular to the line passing through C(0,1) and D(4, -5).

Answer 1

To solve this problem, we will use the two pair of points to find the slope of the equation of each line. Then, by comparing these slopes, we can determine either if they are perpendicular or parallel.

Slope calculations

To calcula the slopes, given the pairs of points, we are going to use the following formula: Given points (a,b) and (c,d) the slope of the line that passes through them is given by the formula

`m=\frac{d\text{ - b}}{c\text{ -a}}=\frac{b\text{ - d}}{a\text{ -c}}`

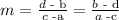
Let us calculate first the slope of the line that passes through the points (7,5) and (-14,-9). In this case, we have a=7,b=5,c=-14 and d=-9. So we get

`m=\frac{5\text{ - (-9)}}{7\text{ - (-14)}}=(14)/(21)=(2\cdot7)/(3\cdot7)=(2)/(3)`

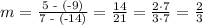
Now, let us calculate the slope of the line that passes through the points (0,1) and (4,-5). In this case, we have a=0,b=1,c=4 and d=-5. So we get

`m=\frac{1\text{ -(-5)}}{0\text{ - 4}}=\frac{6}{\text{ -4}}=\text{ -}(3\cdot2)/(2\cdot2)=\text{ -}(3)/(2)`

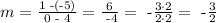
Slope comparison

Now, we compare the slopes to determine if the lines are perpendicular or parallel. Recall that two lines are parallel if they have the same slope and they are perpendicular if the product of their slopes is -1. From our calculations, we can see that the slopes are not equal. Let us confirm that they are perpendicular. To do so, we multiply both slopes. So we get

`(2)/(3)\cdot(\text{ -}(3)/(2))=\text{ -1}`

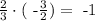
Since their product is -1, this confirms that both lines are perpendicular.