Question

An initial investment of $200 is appreciated for 20 years in an account that earns 6% interest, compounded continuously. Find the amount of money in the account at the end of the period.

Answer 1

To calculate the final amount of money at the end of the period, considering that the interest is compounded continuously you have to use the following formula:

`A=P\cdot e^(rt)`

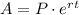
Where

A is the accrued amount at the end of the given time

P is the principal amount

r is the annual nomial interes expressed as a decimal value

t is the time period in years

For this investment, the initial value is P= $200

The interest rate is 6%, divide it by 6 to express it as a decimal value

`\begin{gathered} r=(6)/(100) \\ r=0.06 \end{gathered}`

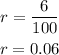
The time is t= 20 years

`\begin{gathered} A=200\cdot e^(0.06\cdot20) \\ A=200\cdot e^{(6)/(5)} \\ A=664.02 \end{gathered}`

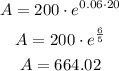
After 20 years, the amount of money in the account will be $664.02