Question

An invester invested a total of 3,300 in two mutual funds. One fund earned a 5% profit while the other earned a 2% profit. If the investor's total profit was $126, how much was invested in each mutual fund?

Answer 1

Given

Total investment of $3,300

5% profit and 2% profit totaling $126

`\begin{gathered} \text{Let} \\ x\text{ be the investment on 5\% profit} \\ y\text{ be the investment on 2\% profit} \end{gathered}`

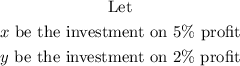
The equations therefore will be

`\begin{gathered} x+y=3300\text{ based on the total amount of investment} \\ 0.05x+0.02y=126\text{ based on the investor's total profit} \end{gathered}`

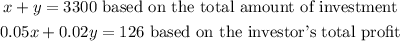
Use substitution method using the first equation

`\begin{gathered} x+y=3300 \\ y=3300-x \\ \\ \text{Substitute }y\text{ to the second equation} \\ 0.05x-0.02y=126 \\ 0.05x-0.02(3300-x)=126 \\ 0.05x-66-0.02x=126 \\ 0.05x-0.02x=126-66 \\ 0.03x=60 \\ (0.03x)/(0.03)=(60)/(0.03) \\ \frac{\cancel{0.03}x}{\cancel{0.03}}=(60)/(0.03) \\ x=2000 \end{gathered}`

Now that we have solve for x, substitute it to the first equation to get the value of y

`\begin{gathered} x+y=3300 \\ 2000+y=3300 \\ y=3300-2000 \\ y=1300 \end{gathered}`

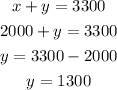
Therefore, the amount invested in mutual fund that earned 5% was $2000, and the amount invested that earned 2% was $1300.