Question

Can you help me answer part A and part B?

Answer 1

Now, Now,We are given the following vectors:

`P\left(5,4\right),Q\left(7,3\right),R\left(8,6\right),S\left(4,1\right)`

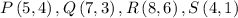
We are asked to determine the following vector:

`PQ+3RS`

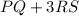
First, we will determine the vector PQ and RS. To determine PQ we use the following:

`PQ=Q-P`

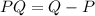
This means we need to subtract "P" from "Q". We do that by subtracting each component of the points, like this:

`PQ=\left(7,3\right)-\lparen5,4)=\left(7-5,3-4\right)`

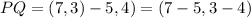
Solving the operations:

`PQ=\left(2,-1\right)`

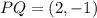
Now, we use a similar procedure to determine RS:

`RS=S-R`

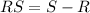
Substituting we get:

`RS=\left(4,1\right)-\left(8,6\right)=\left(4-8,1-6\right)`

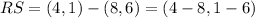
Solving the operations:

`RS=\left(-4,-5\right)`

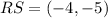
Now, we substitute the values in the vector we are looking for:

`PQ+3RS=\left(2,-1\right)+3\left(-4,-5\right)`

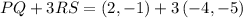
Now, we solve the product by multiplying both components of RS:

`PQ+3RS=(2,-1)+(-12,-15)`

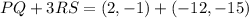
Now, we solve the addition by adding each corresponding component:

`PQ+3RS=(2-12,-1-15)`

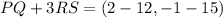
Solving the operations:

`PQ+3RS=(-10,-16)`

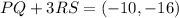
And thus we have determined the components.

Part B. We area asked to determine the magnitude of the vector. To do that we will use the following:

Given a vector of the form:

`X=\left(x,y\right)`

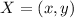
Its magnitude is:

`\lvert X\rvert=√(x^2+y^2)`

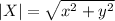
This means that the magnitude is the square root of the sum of the square of the components. Applying the formula we get:

`\lvert\begin{equation*}PQ+3RS\end{equation*}\rvert=√(\left(-10\right)^2+\left(-16\right)^2)`

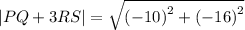
Now, we solve the squares:

`\lvert\begin{equation*}PQ+3RS\end{equation*}\rvert=√(100+256)`

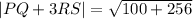
Solving the addition:

`\lvert\begin{equation*}PQ+3RS\end{equation*}\rvert=√(356)`

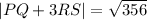
Now, we factor the term inside the radical as follows:

`\lvert PQ+3RS\rvert=√(4\left(89\right))`

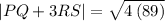
Now, we distribute the radical:

`\lvert PQ+3RS\rvert=√(4)√(89)`

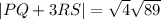
Taking the left square root:

`\lvert PQ+3RS\rvert=2√(89)`

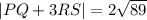
And thus we have determined the magnitude.